C语言02-数据类型和C

1.基本数据类型

1.1整数

1.1.1 int类型

有符号整型，int的值是整数，注意int的取值范围（ISO C规定最小为-32768~32767）

声明：int 变量名;

打印十进制用转换说明%d

1.1.2 其他整数类型

short int 类型：节省空间
long int 或long：适用于较大数值，long是有符号类型
long long int或long long ：是有符号类型，至少占64位
unsigned int或unsigned：只用于非负值
在 C90 标准中,添加了unsigned long int或unsigned long和unsigned int 或unsigned short 类型。C99标准又添加了unsigned long long int或unsigned long long。
在任何有符号类型前面添加关键字signed,可强调使用有符号类型的意图。例如，short、short int、signed short、signed short int 都表示同一种类型。

1.1.3 char类型

用于储存字符，技术层面看char是整数类型，因为其用特定的整数表示特定的字符（计算机用数字编码处理字符）

声明：char 变量名

char 数组可以用于存储字符串，字符串是以空字符 ‘\0’ 结尾的字符序列：char 数组名[]，[]中可以填长度

用单引号括起来的单个字符被称为字符常量，可以是字符、数字和标点符号
用双引号括起来编译器认为是字符串

1.1.4* 非打印字符

一些代表行为的字符，有以下方法打印：

使用ASCII码
使用转义序列

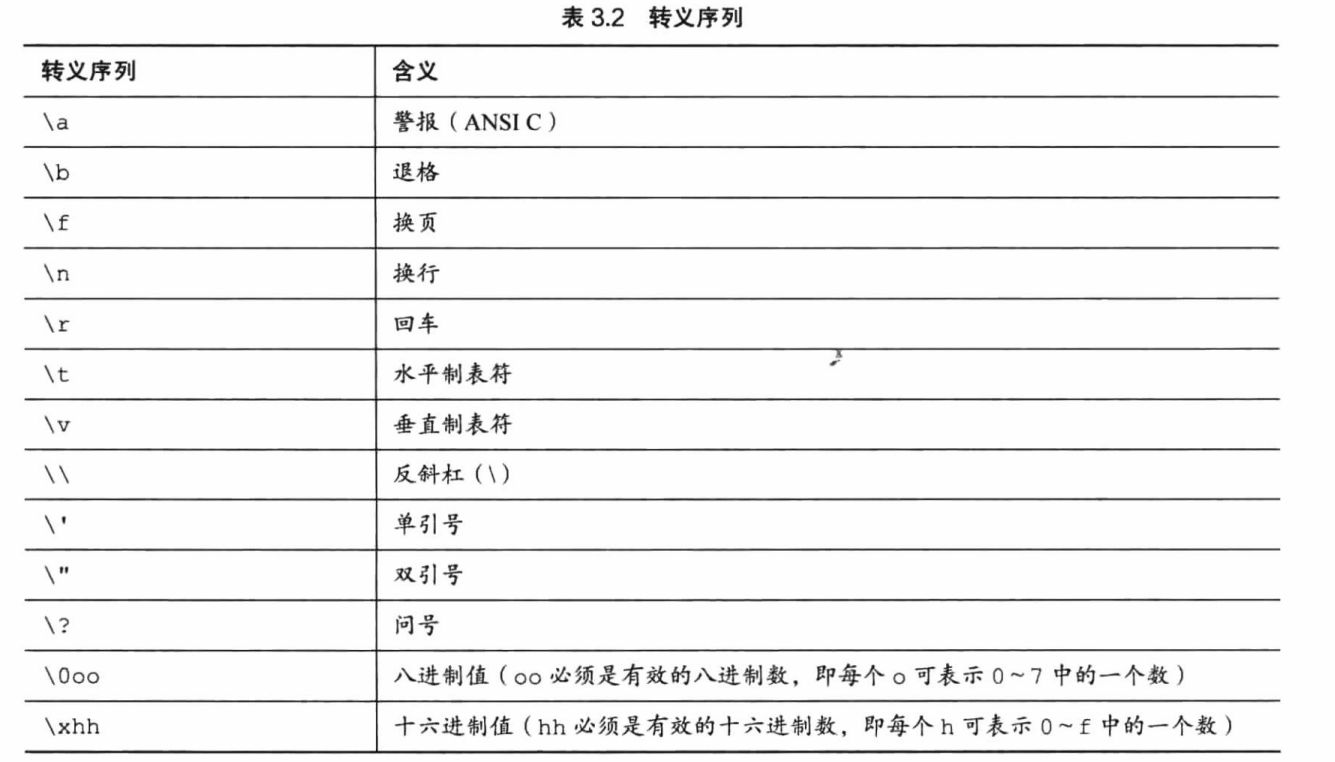
注意把转义序列赋给字符变量时，要用单引号把转义序列括起来，而无论是普通字符还是转义序列，只要是双引号括起来的字符集合，就无需用单引号括起来

1.1.5 _Bool类型

布尔值，即true和false，C语言用1表示true，2表示false

1.1.6 可移植类型stdint.h和inttypes.h

精确宽度整数类型：C创建的新类型名定义在stdint.h头文件中，例如int32_t（32位有符号整数）、uint16_t（16位无符号整数）这些属于精确宽度整数类型，其具有明确的位数，在不同平台上能提高代码的可移植性
最小宽度类型：int_leastN_t和uint_leastN_T系列类型(其中N可以是8/16/32/64，能保证至少具有指定的位数，当需要确保整数类型至少具有一定的位数可以使用，在不同的系统中会选择一种能够满足最小宽度要求的整数类型实现

1.2 浮点数

1.2.1 float、double、long double

float类型必须至少能精确表示6位有效数字，且取值范围至少是10e-37~10e37；

通常系统储存一个浮点数要32位，其中8位用于表示指数的值和符号，剩下24位用于表示非指数部分（尾数或有效数）及其符号

double至少必须能精确表示10位有效数字

对于浮点型常量，编译器默认是double类型的精度，在浮点数后面加上f或F后缀可让编译器将浮点型看做float类型，使用l或L后缀似的其成为long double类型
NaN是一个特殊的浮点值（not a number），其与任何值比较逗返回false，不可用==判断，C99标准中可以用isnan函数来判断一个浮点数是否为NaN

1.2.2 上溢

数值超过该类型所能表示的最大上限时，就会发生上溢；对于浮点数类型，当一个数值变得非常大以至于超出了浮点数的表示范围时，也会发生上溢，通常结果会变为特殊的无穷大值（infinity）表示。

1.3 复数和虚数

复数类型：float_Complex、double_Complex和long double_Complex

虚数类型：是float_Imaginary、double_Imaginary和long double_Imaginary

如果有complex.h头文件，可以用complex代替_Complex，用imaginary代替_Imaginary，还可以用I代替-1的平方根

2.高精度运算*

2.1 高精度输入

输入的数过大，可以用字符做转置处理

示例：

int a[505], b[505], c[505];
int s1[505], s2[505];
int la, lb, lc;
scanf("%s",s1);
scanf("%s",s2);

la = strlen(s1);
lb = strlen(s2);

for (int i=0; i<la; i++){
    a[la-i] = s1[i] - '0';		//字符串转为数字，同时将其倒过来从个位开始加
}
for (int i=0; i<lb; i++){
    b[lb-i] = s2[i] - '0';
}

2.2 高精度加法

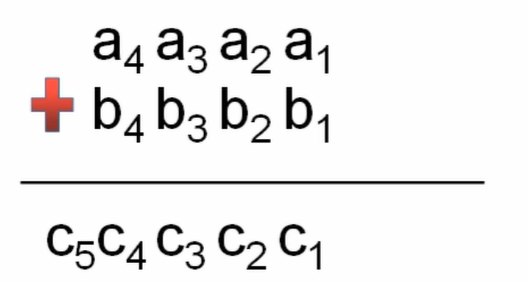
对于图中的运算，算法核心如下：

1
2
3

c[i] += a[i] +b[i]; //对位计算加法
c[i+1] = c[i] / 10; //算出进到下一位的数
c[i] = c[i] % 10; 	//进位完后本位的值

示例：

lc = max(la,lb) + 1;
for (int i=1; i<=lc; i++){
    c[i] += a[i] +b[i]; 
	c[i+1] = c[i] / 10; 
	c[i] = c[i] % 10; 
}

if ( c[lc]==0 && lc>0 ) lc--; //删除前导0

for (int i =lc; i>0; i-- )
    printf("%d", c[i]);		//打印出来

return 0;

2.3 高精度减法

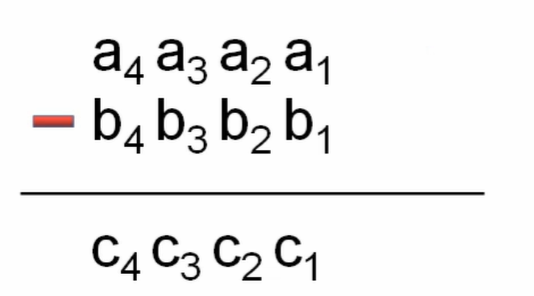
如果a<b，则需要交换a和b，然后再加负号
如果a[i] < b[i]，需要高位借一当十用

if (a[i] < b[i]){
    a[i+1]--;
    a[i] = a[i] + 10;
}
c[i] = a[i] - b[i];

示例：

if ( !compare(s1,s2) ){  //如果s1<s2，则交换两个数
    flag = 1; 	//标记负数
    strcpy(s3,s1);
    strcpy(s1,s2);
    strcpy(s2,s3);
} 
la = strlen(s1);
lb = strlen(s2);

//接下来转置
for (int i=0; i<la; i++)
    a[la-i] = s1[i] - '0';
for (int i=0; i<lb; i++)
    b[lb-i] = s2[i] - '0';
lc = max(la,lb);

for (int i=1; i<=lc; i++){	//主要的减法操作
    if (a[i] < b[i]){	//借位操作
        a[i+1]--;
        a[i]+=10;
    }
    c[i] = a[i] - b[i];
}

while (c[lc]==0 && lc>1) lc--; //删除前导0
if (flag == 1) printf("-");
for (int i=lc; i>0; i--)
    printf("%d", c[i]);

2.4 高精度乘法

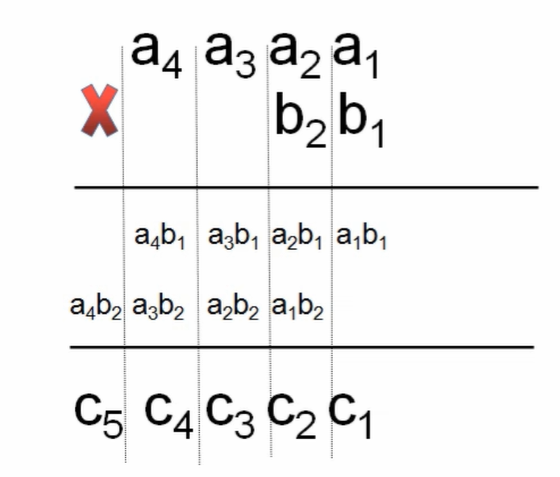
a[i] * b[j] 对应的是c[i+j-1]的位置
注意考虑进位

核心算法：

1
2
3

c[i + j-1] += a[i]*b[i];
c[i+j] += c[i+j-1] / 10;
c[i+j-1] %= 10;

示例：

la = strlen(s1);
lb = strlen(s2);
for(int i=0;i<la;i++)
    a[la-i]= s1[i]-'0';
for(int i=0;i<lb;i++)
    b[lb-i]= s2[i]-'0';
lc = la+lb;

for (int i=1; i<=la; i++){
    for (int j=1; j<=lb; j++){
        c[i + j-1] += a[i]*b[j];
		c[i+j] += c[i+j-1] / 10;
		c[i+j-1] %= 10;
    }
}

if (c[lc]==0 && lc>0) lc--;
for (int i=lc; i>0; i--)
    print ("%d", c[i]);