1. 什么是数据结构

1.1 解决问题方法的效率

数据组织：解决问题方法的效率，跟数据的组织方式有关

空间使用：解决问题方法的效率，跟空间的利用效率有关（例如递归有的时候会导致栈溢出）

算法效率：解决问题方法的效率，跟算法的巧妙程度有关

image-20241016154558142
  • 一种测试代码运行速度的方案：

clock()函数捕捉从程序开始运行到clock()被调用时所耗费的时间。这个时间单位是clock tick（“时钟打点”），在头文件<time.h>中，clock()函数返回的变量类型是clock_t

常数CLK_TCK：机器时钟每秒所走的时钟打点数

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
#include <stdio.h>
#include <time.h>

clock_t start, stop;
double duration;

int main(){
    start = clock();	//开始计时
    MyFunction();	//被测函数
    stop = clock();	//停止计时
    duration = ((double)(stop - start))/CLK_TCK	//计算运行时间
    return 0;
}

1.2 抽象数据类型

即：数据及其相关操作的定义。

可以把抽象数据类型看成是一个模板或约定，告诉我们有哪些数据，以及我们可以对这些数据做哪些操作，但不会告诉我们怎么做。

数据结构：

  • 是数据对象在计算机中的组织方式

    • 逻辑结构
    • 物理存储结构

  • 数据对象必定与一系列加在其上的操作相关联

  • 完成这些操作所用的方法就是算法

抽象数据类型（描述数据结构）：

  • 数据类型：指的是一组数据以及对这些数据可以进行的操作。

    • 数据对象集
    • 数据集合相关联的操作集

  • 抽象：描述数据类型的方法不依赖于具体实现，只描述功能，不描述实现。

    • 与存放数据的机器无关

    • 与数据存储的物理结构无关

    • 与实现操作的算法和编程语言无关

      ​

2. 什么是算法

2.1 算法的定义

算法：一个有限指令集，接受一些输入（有些情况不需要），产生输出，一定在有限步骤之后终止；

每一条指令必须：

  • 有充分明确的目标，不可以有歧义
  • 在计算机能处理的范围之内
  • 描述应不依赖于任何一种计算机语言以及具体的实现手段

2.2 什么是好算法

  • 空间复杂度S(n)：根据算法写成的程序在执行时占用存储单元的长度。这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的
  • 时间复杂度T(n)：根据算法写成的程序在执行时耗费时间的长度。这个长度往往也与输入数据的规模有关。时间复杂度过高的低效算法可能导致我们在有生之年都等不到运行结果。

分析一般算法的效率时，经常关注下面两种复杂度：

image-20241016192854491

​

3. 复杂度的渐进表示法

3.1 表示

image-20241016204857350

复杂度分析小窍门：

image-20241016204942093

大O表示法（O-notation）：描述算法在最坏情况下的运行时间或空间增长情况。它给出了算法执行的上界。

  • 表示方法：O(f(n))，这里 f(n) 是输入规模为 n 时，算法执行时间或空间占用的函数。
  • 作用：用于估算算法在输入数据特别大时性能表现的最坏情况。
  • 例子：
    • O(1)：常数时间，无论输入多大，运行时间保持不变。
    • O(n)：线性时间，输入规模翻倍，算法运行时间也翻倍。
    • O(n^2)：平方时间，输入规模翻倍，运行时间变为原来的四倍。

大Ω表示法（Omega-notation）：描述算法在最优情况下的运行时间或空间增长情况。它给出了算法执行的下界。

  • 表示方法：Ω(f(n))
  • 作用：用于估算算法在输入数据较小时性能表现的最优情况。
  • 例子：
    • Ω(1)：最好的情况是常数时间。
    • Ω(n)：最好的情况是线性时间。

Θ表示法（Theta-notation）：描述算法在输入规模增长时的平均运行时间或空间增长情况。它表示算法的上界和下界都相同，表示算法的准确渐进复杂度。

  • 表示方法：Θ(f(n))

  • 作用：用来准确描述算法的复杂度。

  • 例子：

    • Θ(n)：运行时间正好和输入规模成正比

3.2 分析步骤和例子

3.2.1 具体步骤：

步骤1：确定算法中的基本操作

在分析一个算法时，首先要找出最频繁执行的基本操作。这些操作通常是加法、比较、赋值等。基本操作的执行次数随着输入规模的增大而变化，所以我们关注它们的执行次数。

步骤2：分析每一段代码的执行次数

通常，我们通过分析循环、递归或其他控制结构，来确定不同代码段的执行次数。以下是一些常见结构的时间复杂度：

  • 常数操作：单一的基本操作，如赋值或比较，通常是 O(1)，因为它们只执行一次，不随输入规模变化。
  • 顺序结构：如果一个代码段的各行代码是顺序执行的，比如：
1
2
a = 10;  // O(1)
b = 20;  // O(1)

这些语句都是常数时间 O(1)，总的时间复杂度还是 O(1)。

  • 循环结构：

    单层循环：如果一个循环执行 n 次，比如：

1
2
for i in range(n):
    # O(1) 操作

这个循环中的操作会执行 n 次，所以复杂度是 O(n)。

​ 嵌套循环：如果循环是嵌套的，比如：

1
2
3
for i in range(n):
    for j in range(n):
        # O(1) 操作

最内层的操作会执行 n * n 次，所以复杂度是 O(n^2)。

递归结构：

  • 递归的复杂度需要通过递推公式（递归方程）来解决。例如，对于一个典型的二分搜索算法，它将问题规模每次减半，所以其复杂度方程是 T(n) = T(n/2) + O(1)。通过主定理或展开递推公式，你可以得出时间复杂度为 O(log n)。

步骤3：去除常数项和低阶项

当我们计算出各个代码段的复杂度后，下一步是去除常数项和低阶项。因为渐进复杂度只关心输入规模非常大时的增长趋势，所以我们忽略那些对增长速度影响较小的部分。例如：

  • 5n + 10 的复杂度为 O(n)，因为常数 10 和系数 5 对输入规模的增长影响不大。
  • 2n^2 + 3n 的复杂度为 O(n^2)，因为当 n 非常大时，n^2 比 n 增长得更快，低阶项可以忽略。

步骤4：得出总的时间复杂度

将各个代码段的复杂度加起来，得出算法的总复杂度。如果多个代码段是顺序执行的，我们取其中最大的复杂度作为最终的结果。

​

3.2.2 例子

假设我们有以下代码：

1
2
3
4
5
def example_algorithm(arr):
    n = len(arr)         # O(1)
    for i in range(n):   # 外层循环 O(n)
        for j in range(n):  # 内层循环 O(n)
            print(arr[i], arr[j])  # O(1) 操作

我们来逐步分析：

  1. n = len(arr) 是常数时间操作，复杂度是 O(1)。
  2. 外层循环执行 n 次，每次执行内层循环，所以外层循环的复杂度是 O(n)。
  3. 内层循环也是执行 n 次，每次进行 O(1) 操作，所以内层循环的复杂度是 O(n)。
  4. 因此，总体的复杂度是外层循环和内层循环的乘积，即 O(n * n)，也就是 O(n^2)。
  • 递归算法复杂度计算

递归算法的复杂度通常需要通过递归方程来计算。假设我们有一个计算斐波那契数列的递归算法：

1
2
3
4
5
def fibonacci(n):
    if n <= 1:
        return n  # O(1)
    else:
        return fibonacci(n-1) + fibonacci(n-2)  # 两次递归调用

递归方程可以写作：

  • T(n) = T(n-1) + T(n-2) + O(1)

这种递归会生成一个指数级的调用树，因此其时间复杂度是 O(2^n)。

总结

要计算算法的复杂度，你需要：

  1. 找出基本操作，分析其执行次数。

  2. 分析循环、递归等结构，确定其复杂度。

  3. 去除常数项和低阶项。

  4. 将不同代码段的复杂度相加或取最大值。

    ​

4. 更多应用实例和算法

4.1 实例1-最大子列和问题

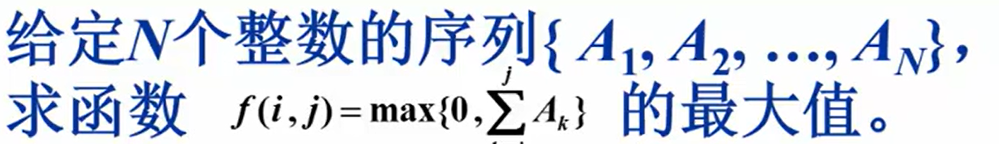
image-20241016211819255
  • 算法1：暴力穷举
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int MaxSubseqSum1(int A[], int N) 
{
    int ThisSum, MaxSum = 0;
    int i, j, k;
    for (i = 0; i < N; i++) { 	/* i 是子列左端位置 */
        for (j = i; j < N; j++) { 	/* j 是子列右端位置 */
            ThisSum = 0; 	/* ThisSum 是从 A[i] 到 A[j] 的子列和 */
            for (k = i; k <= j; k++)  //这一层循环计算了子列和，然而优化方案可以在j的基础上加
                ThisSum += A[k];	
            if (ThisSum > MaxSum) 	/* 如果刚得到的这个子列和更大 */
                MaxSum = ThisSum; 	/* 则更新结果 */
        } 	/* j 循环结束 */
    } 	/* i 循环结束 */
    return MaxSum;
}

这个算法的复杂度T(N) = O(N^3)

算法2：通过优化加法可以更改到O(N^2)….

  • 算法3：分而治之

简介：分而治之（Divide and Conquer）是一种常见的算法设计思想，适用于解决大规模问题。其核心思想是将问题分解为规模较小的子问题，分别解决这些子问题后，再将它们的结果合并，从而得到原问题的解。这种方法的好处是将复杂的问题分成更易处理的小问题，通过递归的方式逐步简化和解决。

示例：将这一个序列从正中间先分开，分别分析左右两边

先分析左边：左边四个从中间断开，以-3和5中间的线为基准

​ -先向左分析4是最大的结果为4

​ -再向右分析到5是最大的结果为5

​ -跨越分界线分析到最大的就是1+5=6（向左到4，向右到5，-3+4+5=6）

再分析右边：右边四个从中间断开，以2和6中间的线为基准

​ -先向左分析到2是最大的结果为2

​ -再向右分析到6是最大的结果为6

​ -跨越分界线得到最大的就是2+6=8

最后跨越一开始的总分界线分析，左边分析到4结果是4，右边分析到6结果是7，得到结果11

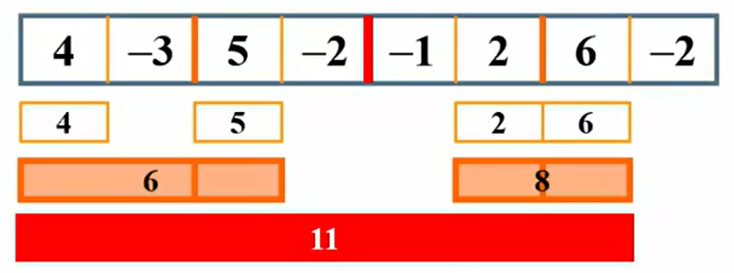
image-20241016213841206

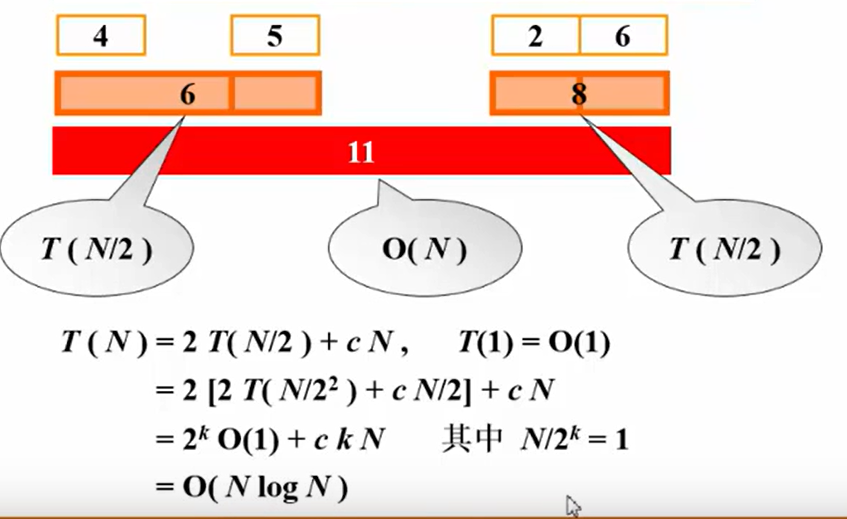
复杂度：

image-20241016215723839
  • 算法4：在线处理

每输入一个数据就进行即时处理，在任何一个地方终止输入，算法都能正确给出当前的解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int MaxSubseqSum4(int A[], int N) 
{
    int ThisSum, MaxSum;
    int i;
    ThisSum = MaxSum = 0;
    for (i = 0; i < N; i++) {
        ThisSum += A[i]; 	/* 向右累加 */
        if (ThisSum > MaxSum)
            MaxSum = ThisSum; 	/* 发现更大和则更新当前结果 */
        else if (ThisSum < 0) 	/* 如果当前子列和为负 */
            ThisSum = 0; 	/* 则不可能使后面的部分和增大，抛弃之 */
    }
    return MaxSum;
}

T(N) = O(N)