信息安全导论02-密码学基础
1. 密码学概述
1.1密码学基本概念
密码学的定义:
- 是结合数学、计算机、信息论等的综合性交叉学科
- 分为密码编码学(cryptography)和密码分析学(cryptanalysis)
- 密码编码学研究如何设计编码使信息只能被指定接收者读懂
- 密码分析学研究如何攻击密码系统,设计和使用密码遵守柯克霍夫准则(算法必须公开,对密钥进行保护)
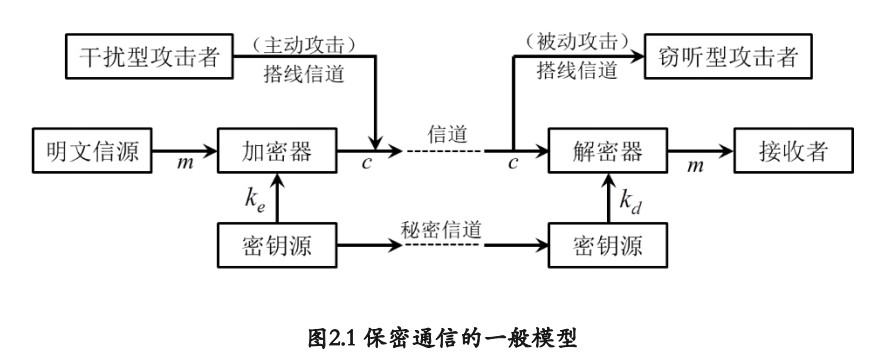
密码体制组成:
- 明文空间M:全体明文集合
- 密文空间C:全体密文集合
- 密钥空间K:全体密钥集合
- 加密算法E:c = E(ke, m)
- 解密算法D:m = D(kd, c)
密码体制分类:
- 对称密码体制:加密密钥ke和解密密钥kd相同
- 非对称密码体制:加密密钥ke和解密密钥kd不同,也称公钥密码
密码体制设计原则:
密码算法安全强度高
安全性依赖于密钥而非算法保密性(柯克霍夫原则)
密钥空间要足够大
易于实现和使用
1.2 密码学发展历史
- 古典密码时期(古代-19世纪末):
- 主要基于手工完成
- 代表:凯撒密码、棋盘密码、栅栏密码等
凯撒密码
凯撒密码是一种替换加密,将明文中的每个字母按照固定位数进行偏移
- 加密公式: 在图中给出的数学表达:
E(ke,m) = (m + n) mod 26
m 是明文字母对应的数值
ke = n 是偏移量
mod 26 确保结果在字母表范围内
- 解密公式:
D(kd,c) = (c - n) mod 26
c 是密文字母对应的数值
kd = n 是偏移量
例如:偏移量是3(ke = kd = 3):明文:It is a secret 密文:LWLVDVHFUHW
- 近代密码时期(20世纪初-50年代末):
- 使用电动机械设备实现加解密
- 代表:Vernam密码(一次性密码本或一次性密钥密码)、Enigma转轮密码机
Vernam密码
Vernam密码是一种完全安全的对称加密算法
基本原理:每个明文字符都与一个随机密钥字符进行异或(XOR)运算,密钥必须与明文等长,密钥必须完全随机,每个密钥只能使用一次
- 现代密码时期(20世纪50年代至今):
- 利用计算机技术实现加解密
- 1949年Shannon的《保密系统的通信理论》标志密码学成为科学
- 1976年Diffie和Hellman提出公钥密码体制
- 代表算法:DES(1977)、RSA(1978)、AES(2001)
1.3 密码体制安全性
攻击类型:
- 穷举攻击:试遍所有可能的密钥
- 统计分析攻击:分析密文和明文的统计规律
- 数学分析攻击:利用算法数学特征进行分析
安全性衡量方法:密码的安全性取决于密钥
计算安全性:最有效攻击算法至少是指数时间
可证明安全性:安全性可归结为数学难题
无条件安全性:即使攻击者计算能力无限也无法破解
2. 对称密码
2.1 分组密码
基本概念:
- 将明文分成固定大小的组进行加密
- 每组明文分别在密钥控制下变成等长密文
基本原理:
- 扩散:明文和密钥的每一位都影响密文多个位
- 混淆:使密文与明文、密钥之间的统计关系复杂化
典型算法——DES:
1977年成为美国数据加密标准,分组长度64比特,密钥56比特,基于Feistel结构
包含初始置换、16轮迭代运算、逆置换
每轮包含扩展置换、与轮密钥异或、S盒代换、P盒置换
SM4算法:
- 中国国家密码算法标准
- 分组长度128比特,密钥长度128比特
- 32轮非线性迭代结构
分组密码工作模式:
- 电子编码本(ECB)模式
- 密码分组链接(CBC)模式
- 密码反馈(CFB)模式
- 输出反馈(OFB)模式
2.2.2 序列密码
基本概念:
- 逐位或逐字节加密
- 密钥序列与明文进行组合
- 有状态密码,加密与当前状态有关
分类:
- 同步序列密码:密钥序列生成独立于明文
- 自同步序列密码:密钥序列依赖于以往密文
组成:
- 密钥序列生成器
- 包含驱动部分和非线性组合部分
典型算法:
- 线性反馈移位寄存器(LFSR)
- 祖冲之序列密码算法(ZUC)
3. 公钥密码
3.1 公钥密码概述
提出背景:
- 对称密码存在密钥分配问题
- 密钥管理复杂,n个用户需要n(n-1)/2个密钥
- 难以实现不可否认功能
基本原理:
- 基于数学函数而非字符操作
- 使用两个独立密钥(公钥和私钥)
- 依赖单向陷门函数
单向陷门函数特性:
- 正向计算容易:给定x,计算y=f(x)容易
- 逆向计算困难:给定y,计算x=f^(-1)(y)困难
- 存在陷门:知道特殊信息δ时可以容易计算逆向
3.2 典型算法
RSA算法:
- 最广泛使用的公钥密码算法
- 可用于加密和数字签名
- 基于大整数分解难题
- 密钥生成步骤:
- 选择两个大素数p、q
- 计算n=pq和φ(n)=(p-1)(q-1)
- 选择公钥e,计算私钥d满足ed≡1 mod φ(n)
- 加密:c≡m^e mod n
- 解密:m≡c^d mod n
SM2椭圆曲线公钥密码算法:
中国国家商用密码标准
基于椭圆曲线密码体制
包含数字签名、密钥交换和公钥加密功能
4. Hash函数
4.1 Hash函数概述
基本概念:
- 将任意长度输入转换为固定长度输出
- 输出称为消息摘要或哈希值
- 是一种单向密码体制
基本性质:
- 可处理任意长度输入
- 输出长度固定
- 计算效率高
- 单向性(抗原像性)
- 抗弱碰撞性(抗第二原像性)
- 抗强碰撞性
- 雪崩效应
4.2 典型Hash算法
MD系列:
- MD2、MD4、MD5
- 输出长度128位
- 由RSA公司设计
SHA系列:
- 美国国家标准
- 不同版本输出长度不同
SM3算法:
- 中国国家密码标准
- 输出长度256位
- 用于数字签名、完整性保护等
4.3 Hash函数应用
消息认证码(MAC):
- 与密钥相关的Hash函数
- 用于验证消息来源和完整性
- 实现方式:
- 基于加密函数的MAC
- 基于Hash的MAC(HMAC)
Merkle树:
- 用于区块链系统
- 快速验证数据完整性
- 二叉树结构,节点为数据Hash值
5. 数字签名
5.1 数字签名概述
基本功能:
- 身份认证
- 数据完整性验证
- 不可否认性
- 匿名性
特点:
- 不可否认性:可验证发送者身份和签名时间
- 不可抵赖性:可验证消息内容
- 可仲裁性:第三方可验证解决争端
与手写签名的区别:
- 签名对象:数字信息vs纸质文件
- 实现方法:数学运算vs字符串附加
- 验证方式:验证算法vs签名对比
- 机密性保护能力:数字签名更优
与加密的区别:
- 加密解密是一次性的
- 签名验证可能需要多次进行
- 签名可能需要长期保存作为法律依据
5.2 典型数字签名算法
- 基于RSA的数字签名:
- 密钥生成:
- 选择大素数p、q
- 计算n=pq,φ(n)=(p-1)(q-1)
- 选择公钥e,计算私钥d
- 签名过程:
- 计算消息hash值h(m)
- 用私钥d计算签名s≡h(m)^d mod n
- 验证过程:
- 计算消息hash值h(m)
- 验证h(m)≡s^e mod n是否成立
- 密钥生成:
6. 密钥管理
6.1 密钥管理概述
密钥分类:
- 会话密钥:用于单次通信
- 密钥加密密钥:用于加密会话密钥
- 主密钥:最高层次密钥
密钥管理层次结构:
- 分层管理
- 不同层次密钥功能和重要性不同
6.2 密钥建立技术
对称密码体制密钥建立:
- 无中心密钥建立
- 基于可信第三方的密钥建立
Diffie-Hellman密钥协商:
- 基于离散对数问题
- 允许双方在不安全信道上建立共享密钥
- 过程:
- 双方分别选择私有数a、b
- 计算并交换公开值g^a mod p、g^b mod p
- 分别计算共享密钥(g^b mod p)^a=(g^a mod p)^b
公钥证书:
- 包含用户身份、公钥等信息
- 由CA签名保证真实性
- 可公开分发和验证
6.3 公钥基础设施(PKI)
组成部分:
- 认证机构(CA)
- 证书和证书库
- 密钥备份和恢复系统
- 密钥和证书更新系统
- 证书历史档案
- 应用接口系统
- 交叉认证
数字证书:
- X.509证书标准格式
- 包含持证主体信息和公钥
- CA签名保证真实性
PKI应用:
- 安全电子邮件(S/MIME)
- PGP(Pretty Good Privacy)
- 提供机密性、完整性和认证服务
7. 本章小结
- 密码学是信息安全的核心基础
- 主要内容包括:
- 分组密码
- 序列密码
- 公钥密码
- Hash函数
- 数字签名
- 密钥管理
- 密码技术是必要但非充分条件,需要配合其他安全措施
以上就是这份密码学基础课件的完整总结。这些内容涵盖了现代密码学的基本概念、主要算法和重要应用,为信息安全提供了理论基础。


