算法与数据结构03-线性结构

1. 顺序表

1.1 概念

线性表（Linear List)：由同类型数据元素构成有序序列的线性结构

• 表中元素个数称为线性表的长度
• 线性表没有元素时，称为空表
• 表起始位置称表头，表结束位置称表尾

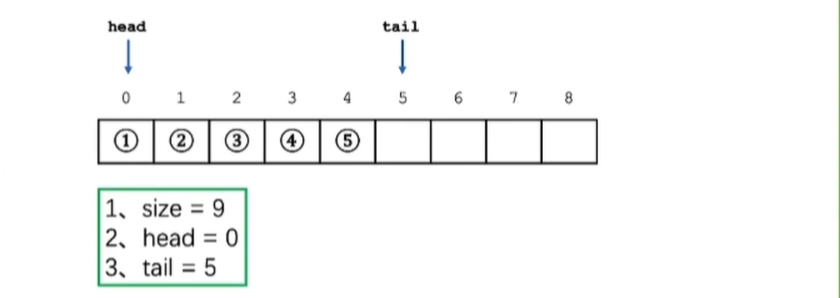
线性表的结构：一段连续的存储空间、两个属性：size（表的大小），count（元素个数）

​

1.2 代码实现

1.2.1 结构定义

typedef struct vector {
	int size, count;	//两个属性
	int* data;			//这段空间(连续的这段存储区)
}vector;

1.2.2 初始化（创建）新表

vector* getNewVector(int n) {	//创建一个新表（返回这个表头的地址）
	vector* p = (vector*)malloc(sizeof(vector));	//开辟顺序表本身的空间（也就是储存size,count,data这三个成员的空间)
	p->size = n;
	p->count = 0;
	p->data = (int*)malloc(sizeof(int) * n);	//创建实际存储数据的数组空间
	return p;
}	//至此获得了一个存储上限为n的顺序表结构

1.2.3 销毁顺序表

void clear(vector* v) {		//销毁顺序表
	if (v == NULL) return;
	free(v->data);
	free(v);
	return;

1.2.4 插入新元素

int insertVector(vector* v, int pos, int val) {	//插入操作，返回一个值代表是否成功
	if (pos < 0 || pos > v->count) return 0;	//插入不成功，位置不合法
	if (v->size == v->count && !expand(v)) return 0;  //插入不成功，因为表满或者扩容失败
	for (int i = v->count - 1; i >= pos; i--) {	//逆序遍历，将插入元素后面的元素向后移
		v->data[i + 1] = v->data[i + 1];
	}
	v->data[pos] = val;
	v->count += 1;
	return 1;
}

1.2.5 删除元素

int eraseVector(vector* v, int pos) {		//删除操作
	if (pos < 0 || pos >= v->count) return 0;
	for (int i = pos + 1;i < v->count;i++) {	//向前移1位
		v->data[i - 1] = v->data[i];
	}
	v->count -= 1;
	return 1;
}

1.2.x 输出顺序表

void outputVector(vector *v) {
	int len = 0;
	for (int i = 0;i < v->size;i++) {
		len += printf("%3d", i);  //技巧：len+=的这种办法可以记录输出长度，以供下面输出横线使用
	}
	printf("\n");
	for (int i = 0; i < len;i++) printf("-");
	printf("\n");
	for (int i = 0;i < v->count;i++) {
		printf("%5d", v->data[i]);
	}
}

1.2.6 扩容操作

int expand(vector* v) {
	if (v == NULL) return 0;
    int *p = (int*)realloc(v->data, sizeof(int) * 2 * v->size);
    if (p == NULL) return 0;
	v->data = p;
	v->size *= 2;
	return 1;
}

​

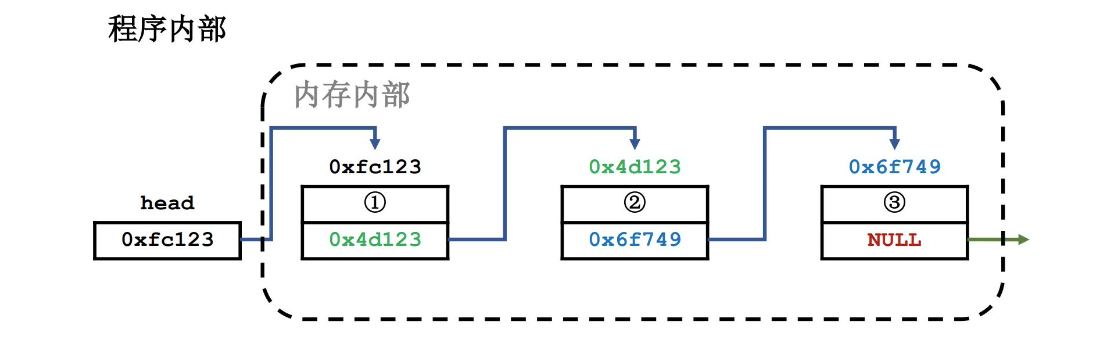
2. 链表

2.1 概念

链表是一种动态的数据结构，由一系列节点组成

每个节点包含两部分：数据域（存储实际数据）和指针域（指向下一个节点）

​

2.2 代码实现

2.2.1 结构定义

typedef struct Node {
	int data;
	struct Node* next;
}Node;

2.2.2 初始化（创建）链表节点

Node* getNewNode(int val) {	//初始化链表节点
	Node* p = (Node *)malloc(sizeof(Node));
	p->data = val;
	p->next = NULL;
	return p;
}

2.2.3 销毁整段链表

void clearNode(Node* head) {
	if (head == NULL) return;
	for (Node* p = head, *q; p; p = q) {	
		q = p->next;	//防止信息丢失
		free(p);
	}
}

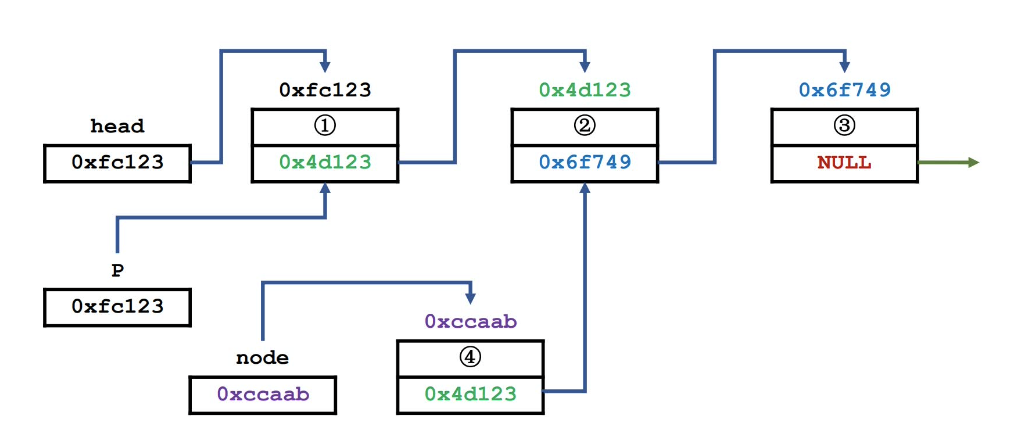
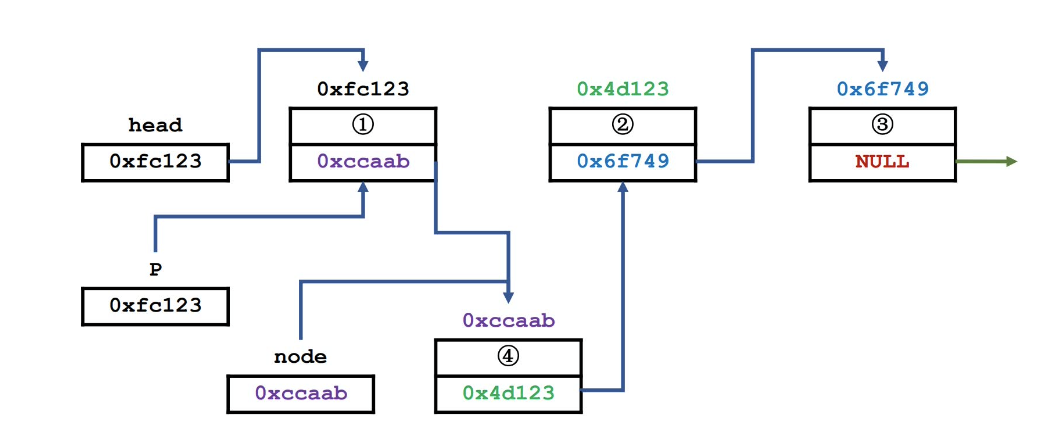
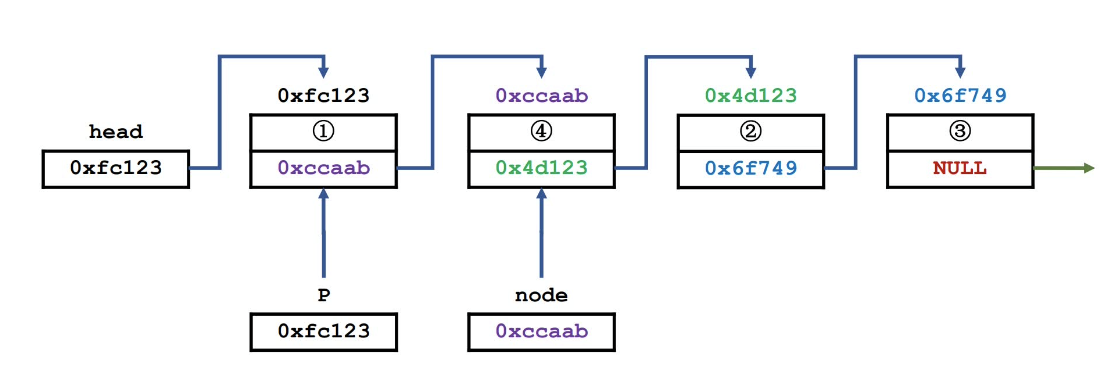
2.2.4 插入链表节点

Node* insert(Node* head, int pos, int val) { //返回值的含义是插入后的链表首地址
	if (pos == 0) {
		Node* p = getNewNode(val);
		p->next = head;
		return p;
	}
	Node* p = head;
	for (int i = 1; i < pos; i++) p = p->next; //p向后走了position - 1步
	Node* node = getNewNode(val);	
	node->next = p->next;
	p->next = node;
	return head;
}

//实现方案2：用有链表改写，更好的方案
Node* insert(Node* head, int pos, int val) { //返回值的含义是插入后的链表首地址
	Node new_head, * p = &new_head;	//虚拟头
	new_head.next = head;	
	Node* node = getNewNode(val);
	for (int i = 0; i < pos; i++) p = p->next;
	node->next = p->next;
	p->next = node;
	return new_head.next;
}

2.2.5 删除链表节点

Node* deleteNode(Node* head, int pos) {	//返回值是删除后链表的头结点地址
    if (head == NULL) return;  // 空链表直接返回
    if (pos == 0) {		//头结点
        Node* temp = head->next;
        free(head);
        return temp;
    }
	// 找到要删除节点的前一个节点
    Node* p = head;	
    for (int i = 1; i < pos && p != NULL; i++) {
        p = p->next;
    }
    if (p == NULL || p->next == NULL) {    // 如果pos超出链表长度
        return head;
    }
    Node* temp = p->next;
    p->next = temp->next;
    free(temp);
    return head;
}

2.2.6 查找

int find1(Node* head, int val) {	//最基础的查找技巧
	Node* p = head;
	while (p) {
		if (p->data == val) return 1;
		p = p->next;
	}
	return 0;
}

​

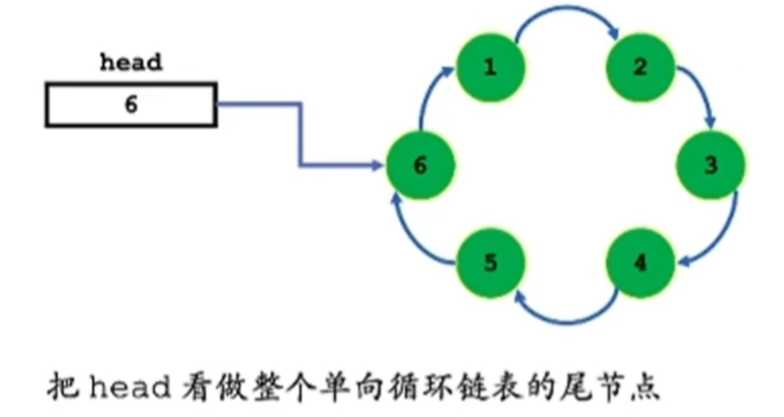
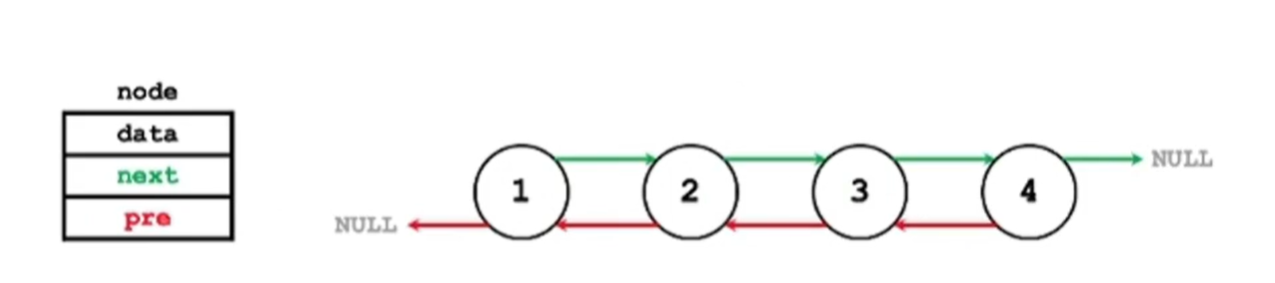
2.3 其他链表

2.3.1 循环链表

2.3.2 双向链表

​

3. 队列

3.1 概念

队列是具有一定操作约束的线性表

• 插入和删除操作：只能在一端插入，而在另一端删除
• 数据插入：入队列 （AddQ）
• 数据删除：出队列（DeleteQ）
• 先来先服务，先进先出（FIFO）

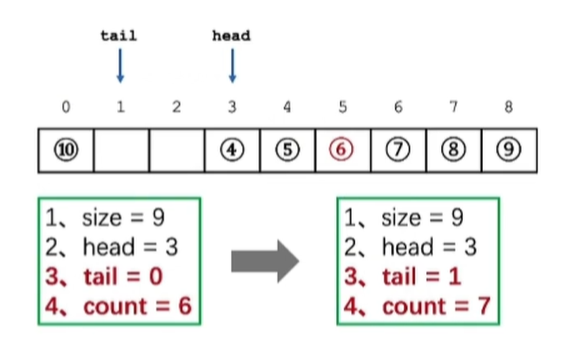
循环队列：更好有效利用空间

​

3.2 代码实现-顺序表

以下假定已经创建了顺序表

3.2.1 结构定义

typedef struct Queue {
	vector* data;	//数据存储区
	int size, head, tail, count;	//循环队列的基础
}Queue;

3.2.2 初始化

Queue* initQueue(int n) {
	Queue* q = (Queue*)malloc(sizeof(Queue));
	q->data = initVector(n);
	q->size = n;
	q->head = q->tail = q->count = 0;
	return q;
}

3.2.3 清除队列

void clearQueue(Queue *q){
	if (q == NULL) return;
	clearVector(q->data);
	free(q);
	return;
}

3.2.4 入队

int push(Queue* q, int val) {  //返回值代表是否成功
	if (q->count == q->size) return 0;
	insertVector(q->data, q->tail, val);
	q->tail += 1;
	if (q->tail == q->size) q->tail = 0;
	q->count += 1;
	return 1;
}

3.2.5 出队

int pop(Queue* q) {
	if (isEmpty(q)) return 0;
	q->head += 1;
    q->count -= 1;
	return 1;
}

3.2.x 队列判空

int isEmpty(Queue* q) {		//判断队列是否空
	return q->count == 0;
}

3.2.x 查看队首元素

int front(Queue* q) {	//查看队首元素
	return vectorSeek(q->data, q->head);
}

​

3.3 代码实现-链表

3.3.1 结构定义

typedef struct Queue {
	Node* l;	//数据存储区
	int size, count;
}Queue;

typedef struct Node {	//节点
    int data;
    Node* next;
}Node;

typedef struct LinkList {
    Node head;	//头结点但不存储数据
    Node* tail; //指向最后一个结点
}LinkList;

3.3.2 初始化

LinkList *initLinklist () {
	Linklist* l = (Linklist *)malloc(sizeof(LinkList));
    l->head.next = NULL;
    l->tail = &(l->head);
    return l;
}

Queue* initQueue() {
	Queue* q = (Queue*)malloc(sizeof(Queue));
	q->l = initLinkList();
	q->count = 0;
	return q;
}

3.3.3 清除队列

void clearLinkList(LinkList *l) {
    //先清除链表头结点后面的那一串
	Node *p = l->head.next, *q;
    while(p){
		q = p->next;
        free(p);
        p = q;
    }
    //再释放掉链表本身
    free(l);
    return;
}

void clearQueue(Queue* q) {
	if (q == NULL) return;
	clearLinkList(q->l);
	free(q);
	return;
}

3.3.4 入队

insertTail(LinkList *l, int val) {
    LinkList *node = getNewNode(val);	//先封装成node结点
    l->tail->next = node;
    l->tail = node;
    return 1;
}

int push(Queue* q, int val) {
	insertTail(q->l, val);
	return 1;
}

3.3.5 出队

int eraseHead(LinkList *l) {
    if (emptyList(l)) return 0;		//判断链表是否空
	Node* p = l->head.next;
    l->head->next = l->head.next->next;
    if (p == l->tail) l->tail = &(l->head);
    free(p);
    return 1;
}

int pop(Queue* q) {
	eraseHead(q->l);
	return 1;
}

​

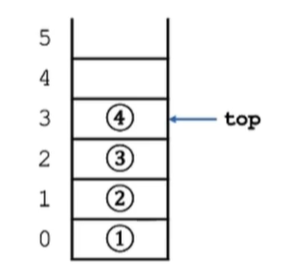
4. 栈

4.1 概念

堆栈（Stack）是一种常见的数据结构，它具有后进先出（Last In, First Out，LIFO）的特性。意思是，最后存入堆栈的数据最先被取出。

• 只在一端（栈顶，Top）做插入、删除
• 插入数据：入栈/压栈（Push）
• 删除数据：出栈/弹栈（Pop）

​

4.2 代码实现-数组顺序表

4.2.1 结构定义

typedef struct Stack {
	int* data;
	int size, top;
}Stack;

4.2.2 初始化

Stack* initStack(int n) {
	Stack* s = (Stack*)malloc(sizeof(Stack));
	s->data = (int*)malloc(sizeof(int) * n);
	s->size = n;
	s->top = -1; //top最开始应该指向0下面的-1位置
	return s;
}

4.2.3 清除栈

void clearStack(Stack* s) {
	if (s == NULL) return;
	free(s->data);
	free(s);
	return;
 }

4.2.4 入栈

int push(Stack* s, int val) {
	if (s->top + 1 == s->size) return 0; //判断是否栈满
	s->top += 1;
	s->data[s->top] = val;
	return 1;
}

4.2.5 出栈

int pop(Stack* s) {
	if (empty(s)) return 0;
	s->top -= 1;
	return 1;
}

4.2.x 判空和查看栈顶元素

int(empty(Stack* s)) {
	return s->top == -1;
}

int top(Stack* s) {
	if (empty(s)) return 0;
	return s->data[s->top];
}

​

4.3 栈的深入理解

4.3.1 引入：括号序列问题

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

题解：典型的栈题（解法略），可以+1抽象为进，-1抽象为出

思维提升：一个（）可以等价为一个完整的事件，( () () ) 可以看做事件之间的包含关系

4.3.2 总结：栈更高维地处理问题

栈可以处理具有完全包含关系的问题