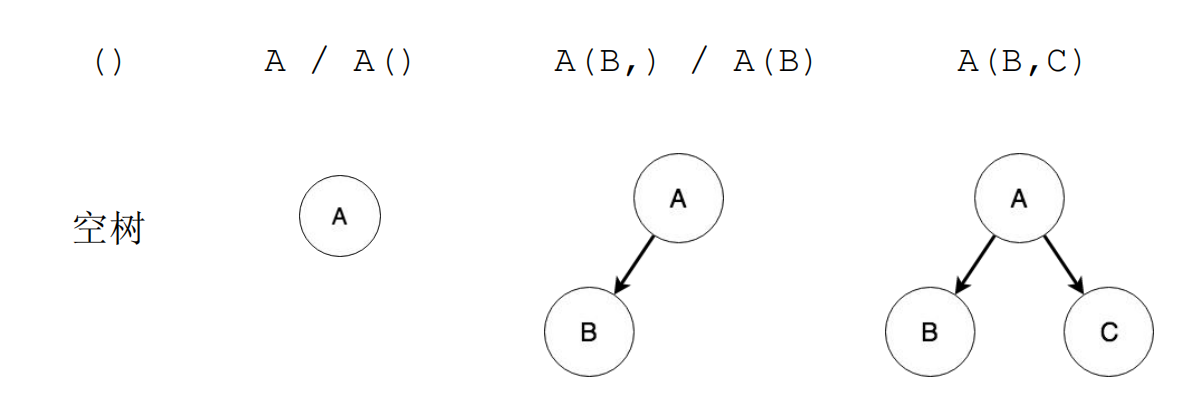
1. 树的基本概念
树是由节点和边组成的数据结构,每个节点可以有多个子节点,但只能有一个父节点
- n叉树:每个节点最多可以有n个子节点
- 树的深度(depth):是指从根节点到最远叶子节点的层数
- 节点的深度:从根节点到该节点的唯一路径上的边的数量
- 节点的高度:从该节点到最远叶子节点的路径上的边的数量
- 节点的度(degree):指它的子节点数量
- 叶子节点(leaf):没有子节点的节点
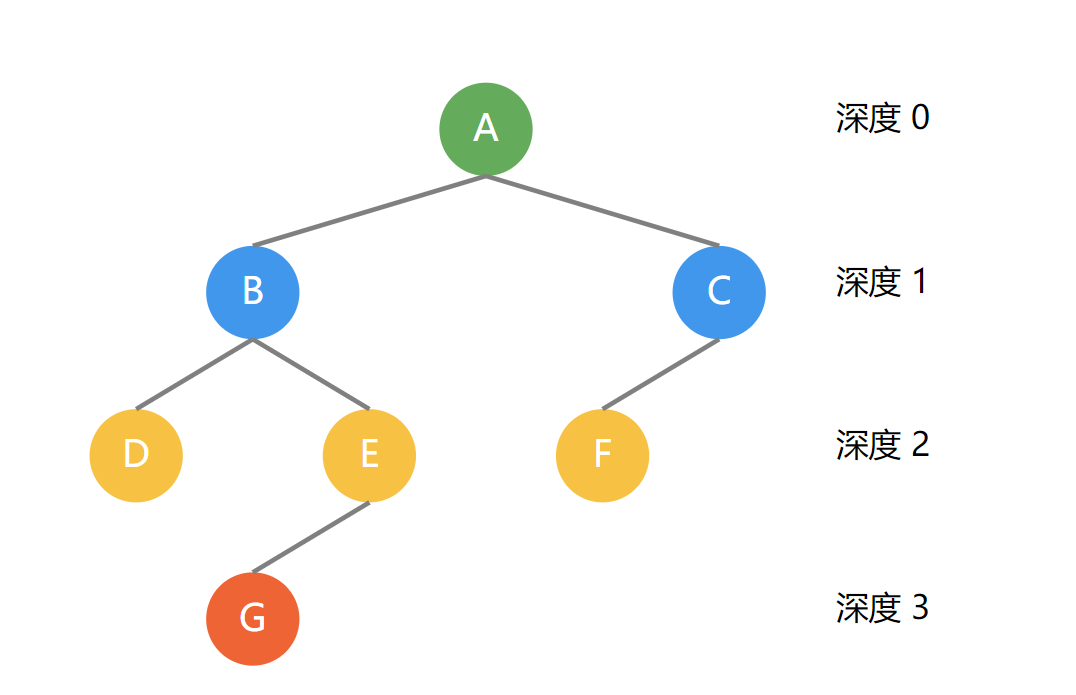
以上图为例,节点B深度=1,高度=2
以上图为例,节点F深度=2,高度=0
核心总结:树的节点代表『集合』,树的边代表『关系』
2. 树形结构的遍历方式
2.1 广度优先遍历(层序遍历)
借用队列,按照层序的方式依次遍历到,具体顺序如下:
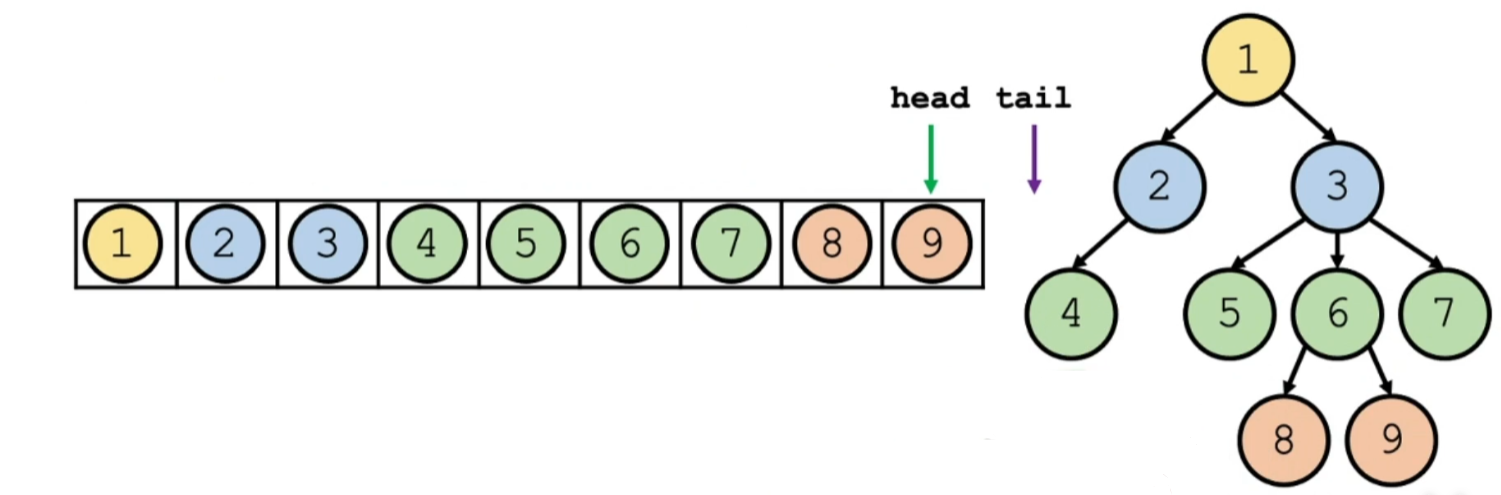
2.2 深度优先遍历
借用栈,对于一个节点只要有一个子节点就将其入栈,直到没有就将相关节点弹栈
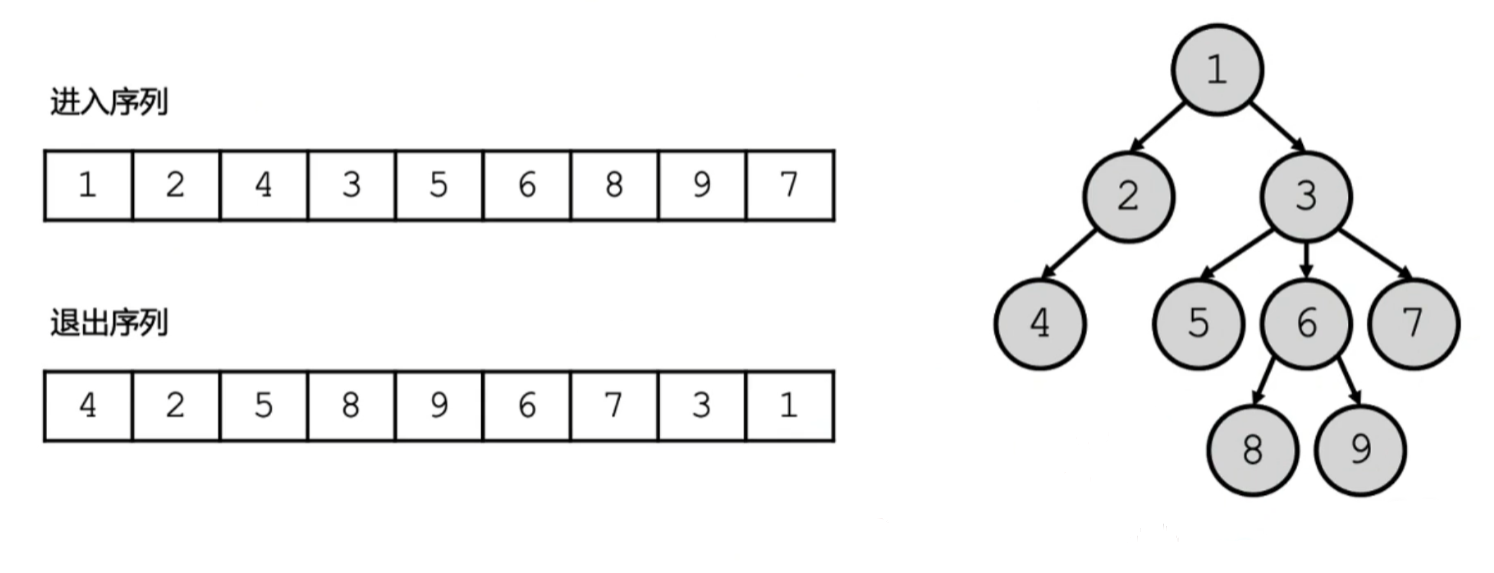
将以上的序列出入做成一张大的时间戳,可以根据区间包含关系,来判断是否是父子关系
例如:对于2号和4号,显然2号的区间内包含4号,故4是2的子节点

3. 二叉树
3.1 概念
二叉树是一种层次化的数据结构,每个节点最多有两个子节点,我们通常称之为左子节点和右子节点。
特殊性质:度为0的节点比度为2的节点多1个
特殊的二叉树类型:
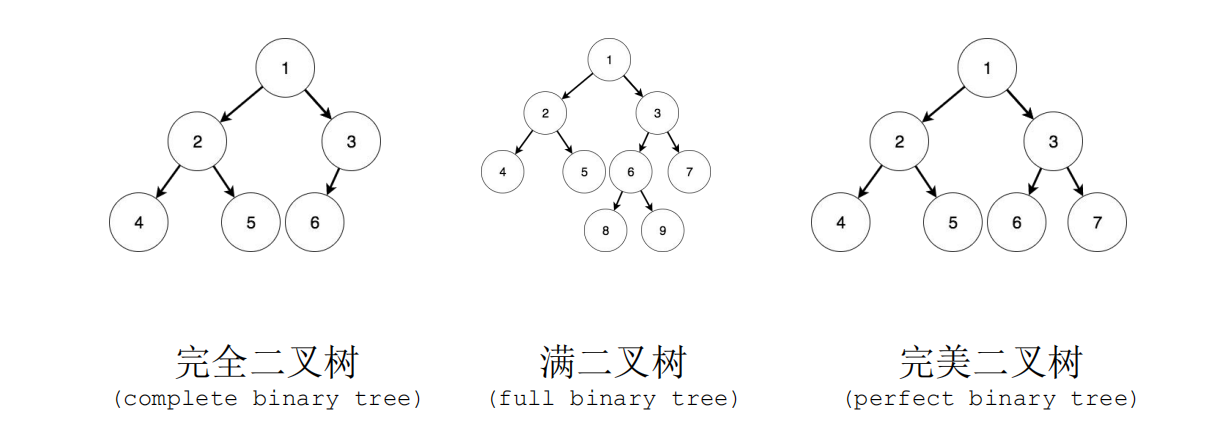
满二叉树:除了叶节点外,每个节点都有两个子节点,所有叶节点都在同一层(没有度为1的节点)
完全二叉树:从上到下、从左到右依次填充节点,最后一层可以不满
完美二叉树:每一层都是满的
平衡二叉树:任意节点的左右子树高度差不超过1
二叉搜索树:左子树所有节点值小于根节点,右子树所有节点值大于根节点
对于完美二叉树:
特性1:编号为i的子节点:
- 左孩子编号:2 * i
- 右孩子编号:2 * i + 1
利用这个特性,我们可以计算得到子节点的地址,而不是指针记录,这样可以节省大量的空间!
特性2:可以用连续空间储存(数组)
3.2 代码实现
3.2.1 结构定义
1
2
3
4
| typedef struct Node {
int key;
struct Node* lchild, * rchild;
} Node;
|
3.2.2 初始化
1
2
3
4
5
6
| Node* getNewNode(int key) {
Node* p = (Node *)malloc(sizeof(Node));
p->key = key;
p->lchild = p->rchild = NULL;
return p;
}
|
3.2.3 清除树
1
2
3
4
5
6
7
| void clear(Node* root) {
if (root == NULL) return;
clear(root->lchild);
clear(root->rchild);
free(root);
return;
}
|
3.2.4 插入
1
2
3
4
5
6
7
8
9
10
11
| Node* insert(Node* root, int key) {
if (root == NULL) return getNewNode(key);
if (rand() % 2) root->lchild = insert(root->lchild, key);
else root->rchild = insert(root->rchild, key);
return root;
}
int main(){
srand(time(0));
return 0
}
|
3.2.5 层序遍历*
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| #define MAX_NODE 10
Node* queue[MAX_NODE + 5];
int head, tail;
void bfs(Node* root) {
head = tail = 0;
queue[tail++] = root;
while (head < tail) {
Node* node = queue[head];
printf("%d", node->key);
if (node->lchild) {
queue[tail++] = node->lchild;
printf("\t%d->%d\n (left)", node->key, node->lchild->key);
}
if (node->rchild) {
queue[tail++] = node->rchild;
printf("\t%d->%d\n (right)", node->key, node->rchild->key)
}
head++;
}
return;
}
|
3.2.6 深度优先遍历*
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int tot = 0;
void dfs(Node* root) {
if (root == NULL) return;
int start, end;
tot += 1;
start = tot;
if (root->lchild) dfs(root->lchild);
if (root->rchild) dfs(root->rchild);
tot += 1;
end = tot;
printf("%d : [%d, %d]\n", root->key, start, end);
return;
}
|
3.3 遍历与线索化
3.3.1 遍历

- 前序: 根 左 右
- 中序: 左 根 右
- 后序: 左 右 根
作用:可以做二叉树的序列化,将一台计算机的数据传入给另外一台计算机,传入的是两种遍历的结果,然后在另一台计算机中恢复二叉树
代码演示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void pre_order(Node* root) {
if (root == NULL) return;
printf("%d ", root->key);
pre_order(root->lchild);
pre_order(root->rchild);
return;
}
void mid_order(Node* root) {
if (root == NULL) return;
mid_order(root->lchild);
printf("%d ", root->key);
mid_order(root->rchild);
return;
}
void post_order(Node* root) {
if (root == NULL) return;
post_order(root->lchild);
post_order(root->rchild);
printf("%d ", root->key);
return;
}
|
3.3.2 线索化
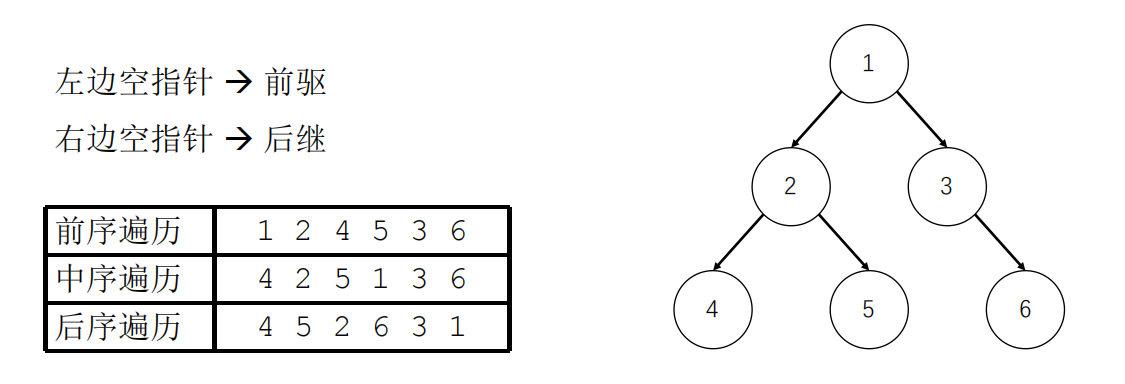
- 前驱:相应节点在相应遍历中的前一个节点
- 后继:相应节点在相应遍历中的后一个节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| typedef struct Node {
int key;
int ltag, rtag;
struct Node* lchild, * rchild;
} Node;
Node* getNewNode(int key) {
Node* p = (Node*)malloc(sizeof(Node));
p->key = key;
p->ltag = p->rtag = 0;
p->lchild = p->rchild = NULL;
return p;
}
void clear(Node* root) {
if (root == NULL) return;
if(root->ltag == 0) clear(root->lchild);
if(root->rtag == 0) clear(root->rchild);
free(root);
}
|
3.4 二叉树:广义表表示法